| Cybernetics: Or the Control and Communication in the Animal and the Machine. Paris, 1948 | Норберт Винер |
|
Кибернетика IV. Обратная связь и колебания |
|
|
В
неврологическую клинику приходит больной. Он не парализован и, получив
приказание, может двигать ногами. Тем не менее он страдает тяжелым
недугом. Он идет странной, неуверенной походкой и все время смотрит
вниз, на землю и на свои ноги. Каждый шаг он начинает с рывка,
выбрасывая вперед сначала одну, потом другую ногу. Если ему завязать
глаза, он не сможет стоять, он шатается и падает. Что с ним?
Приходит другой больной. Пока он неподвижно сидит на стуле, кажется, что
у него все в порядке. Но если предложить ему папиросу, то при попытке
взять её рукой он промахнется. Затем он столь же тщетно качнет руку в
обратном направлении, потом опять вперед, и, наконец, его рука станет
совершать лишь быстрые и бесцельные колебания. Дайте ему стакан воды, и
он выплеснет всю воду, прежде чем сумеет поднести стакан ко рту. Что с
ним?
Оба больные страдают
разными формами так называемой атаксии. Их мышцы достаточно сильны и
здоровы, но они не могут управлять своими движениями. Первый больной
страдает спинной сухоткой. Часть спинного мозга, обычно воспринимающего
ощущения, повреждена или разрушена поздними осложнениями от
сифилиса.
Поступающие сигналы притуплены или даже полностью пропадают. Рецепторы в
суставах, сухожилиях, мышцах и подошвах его ног, обычно сообщавшие ему о
положении и движении ног, не посылают сигналов, которые центральная
нервная система могла бы принять и передать, и чтобы получить информацию
о положении своего тела, больной должен полагаться на глаза и органы
равновесия внутреннего уха.
Физиолог на своем языке скажет, что больной
потерял значительную часть проприоцептивных и кинестетических ощущений.
Второй больной не потерял проприоцептивных ощущений – у него повреждение
мозжечка, и он болен так называемым мозжечковым, или интенционным,
тремором. По-видимому, функция мозжечка – соразмерять мышечную реакцию с
проприоцептивными сигналами, и если эта соразмерность нарушена, одним из
следствий может явиться тремор.
Мы видим, таким образом,
что для эффективного воздействия на внешний мир не только необходимо
иметь хорошие эффекторы, но действие этих эффекторов должно находиться
под надлежащим контролем центральной нервной системы; показания же
контрольных органов должны сочетаться надлежащим образом с другими
сведениями, поступающими из органов чувств, образуя правильно
соразмеренные выходные сигналы к эффекторам. Нечто подобное
наблюдается и в механических системах.
Рассмотрим центральный пост сигнализации на железной дороге. Оператор управляет рядом рычагов, которые открывают или закрывают семафоры и переводят стрелки. Однако он не может слепо верить, что семафор и стрелки подчинились его приказаниям. Стрелки могли замерзнуть или снег мог согнуть крылья семафоров, и действительное положение стрелок и сигналов семафоров – эффекторов оператора – может не соответствовать его приказаниям. Во избежание опасностей, неизбежно связанных с такой возможностью, каждый эффектор – стрелка или сигнал семафора – соединяется с контрольными приборами на сигнальном посту, которые сообщают оператору о действительном состоянии и работе эффектора. Это представляет собой механическую аналогию повторению приказов в военно-морском флоте, где по уставу каждый подчиненный по получении приказа повторяет его своему начальнику, чтобы показать, что он расслышал и понял. На основании таких повторенных приказов и действует оператор. Заметим, что в этой системе человек участвует в цепи прямой и обратной передачи информации, в цепи, которую мы далее будем называть цепью обратной связи. Правда, оператор не может действовать полностью по своему произволу; стрелки и сигналы связаны блокировкой, механической или электрической, и не в его воле выбрать гибельные комбинации. Но имеются цепи Обратной связи, в которых человек совершенно не участвует. Одна из таких цепей – обычный термостат, регулирующий отопление жилища. Термостат устанавливают на желательную температуру помещения, и если действительная температура ниже, то срабатывает устройство, которое открывает заслонку печи для усиления тяги или увеличивает поступление горючего и тем самым доводит температуру помещения до желательного уровня. Если же температура помещения превышает желательный уровень, то выключается тяга, либо уменьшается или прекращается поступление горючего. Таким образом, температура помещения удерживается приблизительно на постоянном уровне. Заметим, что постоянство этого уровня зависит от качества конструкции термостата и что плохо спроектированный термостат может вызвать сильные колебания температуры, подобные движениям человека, страдающего мозжечковым тремором. Другой пример чисто механической системы обратной связи – это изученный впервые Кларком Максвеллом регулятор паровой машины, служащий для регулировки её скорости при переменных режимах нагрузки. регулятор в своем первоначальном виде, как его сконструировал Уатт, состоит из двух шаров, укрепленных на маятниковых стрежнях на противоположных сторонах вращающегося вала. Собственный вес или пружина тянет шары вниз, а центробежная сила, зависящая от угловой скорости вала, стремится подбросить их вверх. Поэтому они принимают некоторое промежуточное положение, которое также зависит от угловой скорости. Шары через другие стержни управляют положением муфты, сидящей на валу, которая приводит в движение золотник, открывающий впускные клапаны цилиндра, когда скорость машины уменьшается и шары опускаются, и закрывающий их, когда скорость машины увеличивается и шары поднимаются. Заметим, что обратная связь стремится противодействовать тому, что делает система; следовательно, эта обратная связь является отрицательной. Итак, мы рассмотрели примеры отрицательной обратной связи для стабилизации температуры и отрицательной обратной связи для стабилизации скорости. Возможна также отрицательная обратная связь для стабилизации положения, как в рулевых машинах корабля, которые приходят в действие при наличии угловой разности между положением штурвала и положением руля и действуют всегда таким образом, чтобы привести положение руля в соответствие с положением штурвала. Обратная связь при произвольных действиях человека имеет такой же характер. Мы не хотим специально приводить в движение определенные мышцы и даже вообще не знаем, какие мышцы нужно привести в движение, чтобы выполнить данную задачу, мы просто хотим взять предмет. Наше движение регулируется степенью того, насколько задача ещё не выполнена. Информация, поступающая обратно в управляющий центр, стремится противодействовать отклонению управляемой величины от управляющей, но она может зависеть от этого отклонения весьма различным образом. Простейшие управляющие системы – линейные системы: выходной сигнал исполнительного органа зависит линейно от входного сигнала, и при сложении входных сигналов складываются и выходные сигналы. Выходной сигнал отсчитывается каким-нибудь прибором, также линейным. Этот отсчет просто вычитается из входного сигнала. Мы хотим дать точную теорию работы такой системы и, в частности, исследовать её неисправное поведение и возникновение в ней колебаний при неправильном обращении или перегрузке. В этой книге мы по возможности избегали математической символики и математических методов, хотя в ряде мест, включая предыдущую главу, вынуждены были примириться с ними. Сейчас речь опять пойдет о вопросах, где математическая символика – самый надежный язык; избежать её можно только ценой длинных перифраз, которые вряд ли будут понятны профану и которые поймет лишь читатель, знакомый с математической символикой, поскольку в его власти перевести их в символы. Наилучший компромисс, который мы можем выбрать, – это дополнять символику пространными словесными пояснениями. Пусть f(t) – функция времени t, где t изменяется от – ∞ до ∞; иначе говоря, f(t) – величина, принимающая определенное числовое значение для каждого момента t. В любой момент t нам доступны величины f(s), где s меньше или равно t, но отнюдь не больше t. Мы располагаем устройствами, электрическими или механическими, которые задерживают входной сигнал на фиксированное время и выдают нам при входном сигнале f(t) выходной сигнал f(t–τ), где τ – фиксированная задержка. Мы можем включить одновременно несколько таких устройств, получив на выходах сигналы f(t–τ1), f(t–τ2),..., f(t–τn). Каждый из этих выходных сигналов мы можем умножить на фиксированные величины, положительные или отрицательные. Так, при помощи потенциометра можно умножить напряжение на фиксированное положительное число, меньшее единицы, и не очень трудно изобрести автоматические компенсационные устройства и усилители, чтобы умножать напряжение на отрицательные величины или на величины, большие единицы. Нетрудно также составить простую электрическую схему для непрерывного сложения напряжений, при помощи которой мы получим выход Увеличивая число задержек τk и выбирая подходящим образом коэффициенты ak, мы можем сколь угодно приблизиться к выходному сигналу вида 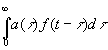 (4.02)
(4.02)
Обратим внимание на то существенное обстоятельство, что в этом выражении интегрирование производится от 0 до ∞, а не от – ∞ до ∞. В противном случае мы могли бы с помощью различных практических устройств преобразовать наш сигнал в f(t+σ), где σ положительно. Но это предполагает знание будущего функции f(t), a f(t) может быть величиной, которая не определяется однозначно своим прошлым; пример – координаты трамвая, который может повернуть на стрелке в ту или другую сторону. Если физический процесс по видимости дает нам оператор, преобразующий f(t) в где а(τ) не исчезает при отрицательных τ, это значит, что мы не имеем больше истинного оператора для f(t),определяемого однозначно прошлым этой функции. Такое может встретиться в реальных физических ситуациях. Например, динамическая система без входа может прийти в постоянные колебания или даже в колебания, нарастающие до бесконечности, с неопределенной амплитудой. В этом случае будущее системы не определяется её прошлым, и мы, наверное, можем найти формализм, в котором бы использовался оператор, зависящий от будущего. Операция, посредством которой получено выражение (4.02) из f(t), имеет ещё два существенных свойства: 1) она не зависит от сдвига начального момента и 2) она линейна. Первое свойство выражается утверждением, что если 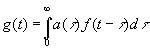 (4.04)
(4.04)
то 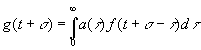 (4.05)
Второе выражается утверждением, что если
(4.05)
Второе выражается утверждением, что если
то 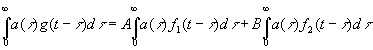 (4.07)
(4.07)
Можно показать, что в некотором подходящем смысле всякий оператор для прошлого функции f(t), линейный и инвариантный относительно сдвига начального момента, имеет вид (4.02) или является пределом последовательности операторов этого вида. Например, f’(t) есть результат применения оператора с такими свойствами к f(t), и потому 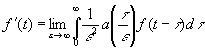 (4.08)
(4.08)
где 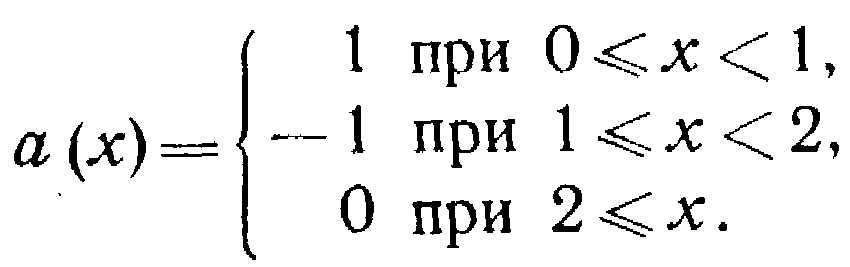 (4.09)
(4.09)
Как мы уже видели, функции еzt составляют особенно интересное семейство с точки зрения оператора (4.02), поскольку и оператор задержки становится просто множителем, зависящим от z. Оператор (4.02) переходит тогда в 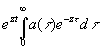 (4.11)
(4.11)
и также оказывается оператором умножения, зависящим только от z. Выражение 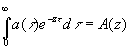 (4.12)
(4.12)
называется представлением, оператора (4.02) в виде функции частоты. Если z – комплексная величина х+iy, где х и y – действительные числа, то (4.12) переходит в 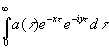 (4.13)
(4.13)
Отсюда следует ввиду известного неравенства Шварца для интегралов, что если y>0 и 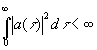 (4.14)
(4.14)
то 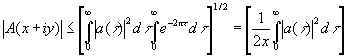 (4.15)
(4.15)
Это значит, что А(х+iу) – ограниченная голоморфная функция комплексной переменной в каждой полуплоскости x≥ε>0, а функция A(iy) представляет в некотором весьма определенном смысле граничные значения этой функции. Положим где и и v – действительные числа. Тогда x+iy определится как функция (не обязательно однозначная) от u+iv. Это функция аналитическая, хотя и мероморфная, за исключением точек u+iv, соответствующих точкам z=x+-iy, где дА(z)/дz=0. Граница х=0 перейдет в кривую с параметрическим уравнением 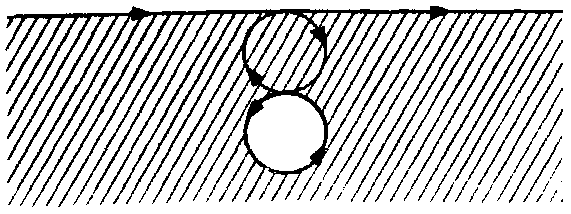 Эта новая кривая может пересекать саму себя любое число раз, но в общем
случае она будет делить плоскость на две области. Рассмотрим кривую
(4.17), вычерченную в направлении возрастания у от –∞ до +∞. Если идти
от неё вправо по непрерывной линии, не пересекающей снова кривую (4.17),
можно попасть в те или иные точки плоскости.
Точки, не входящие в это
множество и не лежащие на кривой (4.17), мы будем называть внешними
точками. Часть кривой (4.17), содержащую предельные точки внешних точек,
назовем эффективной границей. Все остальные точки будут именоваться
внутренними точками. На нашем чертеже с границами, проведенными в
направлении стрелок (рис. 1), внутренние точки заштрихованы, а
эффективная граница выделена жирной линией.
Условие ограниченности
функции А в любой правой полуплоскости указывает на то, что бесконечно
удаленная точка не может быть внутренней точкой. Она может быть
граничной точкой, хотя существуют весьма определенные ограничения на тип
граничной точки, которой может быть бесконечно удаленная точка.
Эти
ограничения касаются “толщины” множества внутренних точек,
простирающихся к бесконечности.
Мы переходим теперь к
математической формулировке задачи о линейной
обратной связи. Пусть
структурная (не электрическая!) схема нашей системы имеет вид, как на
рис. 2. Эта новая кривая может пересекать саму себя любое число раз, но в общем
случае она будет делить плоскость на две области. Рассмотрим кривую
(4.17), вычерченную в направлении возрастания у от –∞ до +∞. Если идти
от неё вправо по непрерывной линии, не пересекающей снова кривую (4.17),
можно попасть в те или иные точки плоскости.
Точки, не входящие в это
множество и не лежащие на кривой (4.17), мы будем называть внешними
точками. Часть кривой (4.17), содержащую предельные точки внешних точек,
назовем эффективной границей. Все остальные точки будут именоваться
внутренними точками. На нашем чертеже с границами, проведенными в
направлении стрелок (рис. 1), внутренние точки заштрихованы, а
эффективная граница выделена жирной линией.
Условие ограниченности
функции А в любой правой полуплоскости указывает на то, что бесконечно
удаленная точка не может быть внутренней точкой. Она может быть
граничной точкой, хотя существуют весьма определенные ограничения на тип
граничной точки, которой может быть бесконечно удаленная точка.
Эти
ограничения касаются “толщины” множества внутренних точек,
простирающихся к бесконечности.
Мы переходим теперь к
математической формулировке задачи о линейной
обратной связи. Пусть
структурная (не электрическая!) схема нашей системы имеет вид, как на
рис. 2.
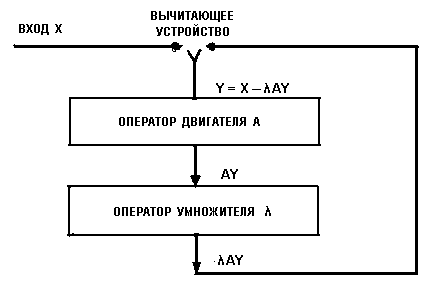 Здесь входной сигнал
двигателя, обозначенный через Y, равен разности между первоначальным
входным сигналом Х и выходным сигналом умножителя, умножающего выходную
мощность AY двигателя на коэффициент λ. Тогда
Здесь входной сигнал
двигателя, обозначенный через Y, равен разности между первоначальным
входным сигналом Х и выходным сигналом умножителя, умножающего выходную
мощность AY двигателя на коэффициент λ. Тогдаи откуда выходной сигнал двигателя Следовательно, оператор, создаваемый всем механизмом обратной связи, равен A/(1+ λA). Он будет бесконечно большим тогда и только тогда, когда А= –1/λ. Κπивая (4.17) для этого нового оператора будет иметь вид и ∞ будет внутренней точкой этой кривой тогда и только тогда, когда –1/λ является внутренней точкой первоначальной кривой (4.17) [Речь идет о точке (–1/λ, 0) на плоскости (u, v)]. В этом случае обратная связь с коэффициентом λ, несомненно, произведет нечто катастрофическое, и эта катастрофа практически выразится в том, что система придет в неограниченные, нарастающие колебания. Если же точка –1/λ внешняя, то можно показать, что никаких неприятностей не будет, и обратная связь будет устойчивой. Случай, когда точка –1/λ лежит на эффективной границе, требует особого исследования. В большинстве случаев система может прийти при этом в колебание с амплитудой, которая не будет увеличиваться. Пожалуй, полезно рассмотреть несколько операторов А и допустимые для них диапазоны обратной связи. Мы будем рассматривать не только операции (4.02), но и их пределы, предполагая, что к последним применимы те же рассуждения. Если оператор А соответствует дифференциальному оператору, то A(z)=z; тогда при изменении у от – ∞ до ∞ точно так же изменяется и А (у), и внутренние точки являются внутренними точками правой полуплоскости. Точка –1/λ всегда является внешней, и любая степень обратной связи возможна. Если то кривая (4.17) принимает следующий вид: или что можно также записать в виде Таким образом, наша кривая есть окружность с радиусом 1/2 и центром в точке (1/2, 0). Обход её совершается по часовой стрелке, и внутренними будут те точки, которые обычно считаются внутренними. В этом случае обратная связь также неограниченна, ибо точка – 1/λ всегда находится вне круга. Оператор a(t), соответствующий этому оператору А, будет равен Положим теперь тогда (4.17) принимает вид 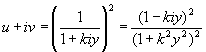 (4.28)
(4.28)
Или что дает или Тогда 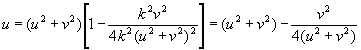 (4.32)
(4.32)
В полярных координатах при u = ρ соs φ, v = ρ sin φ получим или Иными словами Можно показать, что оба эти уравнения изображают одну кривую – кардиоиду с вершиной в начале координат и острием, направленным вправо. Внутренняя область этой кривой не содержит точек отрицательной действительной оси; как и в предыдущем случае, допустимое усиление неограниченно. Оператор а(t) для этого случая имеет следующий вид: Положим ещё Определим ρ и φ, как в предыдущем случае. Тогда Как в первом случае, отсюда получим т.е. 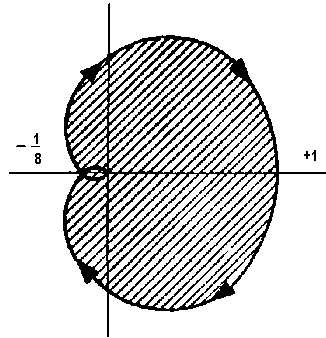 Эта кривая имеет форму, показанную на
рис.3. [Кривая ρ1/3=cos φ/3 называется
кэлиевой кривой 6-го порядка (по имени английского математика А.
Кэли).
И кардиоида, и кэлиева кривая 6-го порядка суть частные случаи
так называемых синус-спиралей].
Заштрихованная область изображает внутренние точки. Коэффициент обратной
связи не может быть больше 1/8. Соответствующий оператор a(t) равен Эта кривая имеет форму, показанную на
рис.3. [Кривая ρ1/3=cos φ/3 называется
кэлиевой кривой 6-го порядка (по имени английского математика А.
Кэли).
И кардиоида, и кэлиева кривая 6-го порядка суть частные случаи
так называемых синус-спиралей].
Заштрихованная область изображает внутренние точки. Коэффициент обратной
связи не может быть больше 1/8. Соответствующий оператор a(t) равен
и Кривая (4.17) в этом случае представляет собой единичную окружность с центром в начале координат, проходимую в направлении часовой стрелки со скоростью, равной единице. Внутренней областью кривой будет внутренняя область в обычном смысле, и предельная обратная связь равна 1. Отсюда можно вывести одно весьма интересное заключение Оператор 1/(1+kz) можно компенсировать произвольно сильной Обратной связью, что заставляет A/(1+λA) приближаться сколь угодно близко к единице в сколь угодно широком диапазоне частот. Таким образом, три последовательных оператора этого типа можно компенсировать тремя – или даже двумя – обратными связями. Но оператор 1/(1+kz)3, получаемый при последовательном соединении трех операторов 1/(1+kz), нельзя сколь угодно точно компенсировать одной Обратной связью. Оператор 1/(1+kz)3 можно также записать в виде и рассматривать как предел аддитивного соединения трех операторов со знаменателями первой степени. Итак, оказывается, что сумму различных операторов, каждый из которых допускает сколь угодно точную компенсацию одной обратной связью, нельзя компенсировать таким же образом. В ценной книге Маккола приведен пример сложной системы, которая может быть стабилизирована двумя обратными связями, но не одной. Речь идет о системе управления кораблем при помощи гирокомпаса. Наличие угла между курсом, который задал рулевой, и тем, который показывает компас, приводит к перекладке руля, создающей вследствие поступательного движения корабля вращающий момент, который изменяет курс корабля таким образом, чтобы уменьшить расхождение между заданным и действительным курсом. Если это осуществляется путем непосредственного открывания клапанов одной рулевой машины и закрывания клапанов другой с таким расчетом, что скорость перекладывания руля пропорциональна отклонению корабля от курса, то угловое положение руля будет примерно пропорционально моменту вращения корабля и, следовательно, его угловому ускорению. Поэтому поворот корабля пропорционален с отрицательным коэффициентом третьей производной отклонения от курса, а операция, которую нужно стабилизировать обратной связью от гирокомпаса, имеет вид kz3, где k положительно. Таким образом, мы получаем для кривой (4.17) уравнение и поскольку внутренней областью служит левая полуплоскость, никакой следящий механизм не сможет стабилизировать эту систему. В этом описании мы несколько упростили задачу управления. В действительности здесь присутствует какое-то трение, и сила, поворачивающая корабль, не определяет ускорения. Если θ – угловое положение корабля, а φ – угловое положение руля по отношению к кораблю, то и Эту кривую можно записать как и систему по-прежнему нельзя стабилизировать никакой обратной связью. Когда у изменяется от –∞ до ∞, v изменяется от ∞ до – ∞, так что внутренняя область кривой расположена слева. Если, с другой стороны, положение руля пропорционально отклонению от курса, то оператор, который мы хотим стабилизировать обратной связью, имеет вид k1z2+k2z, и кривая (4.17) будет задаваться уравнением Эту кривую можно записать как но на этот раз при изменении у от – ∞ до ∞ и также изменяется от – ∞ до ∞, а кривая наша обходится в направлении от у= – ∞ до у= ∞. Внешняя область кривой находится слева от неё, и возможно неограниченное усиление. Для достижения этого результата можно применить вторую ступень обратной связи. Если положение клапанов рулевой машины регулируется не расхождением между действительным и желательным курсом, а разностью между этой величиной и угловым положением руля, то при достаточно большой обратной связи (т.е. когда клапаны открыты достаточно широко) будет поддерживаться с любой точностью пропорциональность между угловым положением руля и отклонением корабля от истинного курса. Система управления с двойной обратной связью обычно и применяется для автоматического управления кораблем при помощи гирокомпаса. В человеческом теле движение руки или пальца связано с большим числом суставов. Выходное усилие равно векторной комбинации выходных усилий всех этих суставов. Мы видели, что, вообще говоря, сложную аддитивную систему такого рода нельзя стабилизировать одной обратной связью. Поэтому обратная связь произвольного движения, при помощи которой мы регулируем выполнение задачи, наблюдая, насколько та ещё не выполнена, должна быть поддержана другими обратными связями. Последние называются обратными связями позы и служат общему поддержанию тонуса мышечной системы. Именно обратная связь произвольного движения и подвержена нарушениям и расстройствам при повреждении мозжечка, ибо следующий за этим тремор появляется только тогда, когда больной пытается выполнить произвольное действие. Этот интенционный тремор, при котором больной не может взять стакан воды, не опрокинув его, весьма отличен по природе от тремора при паркинсоновской болезни, или дрожательном параличе. Тремор при паркинсоновской болезни проявляется наиболее типично, когда больной неподвижен, и часто, по-видимому, значительно ослабляется, когда больной пытается выполнить сознательно контролируемые действия. Встречаются хирурги с паркинсоновской болезнью, которые неплохо справляются с операциями. Паркинсоновская болезнь, как известно, имеет причину не в болезненном состоянии мозжечка, а связана с патологическим очагом где-то в стволе мозга. Это лишь одна из болезней обратных связей позы, и многие из таких болезней происходят от повреждений частей нервной системы, расположенных весьма разнообразно. Одна из важных задач физиологической кибернетики – распутать и локализировать различные части этого комплекса обратных связей произвольных действий и поз. Примерами составных рефлексов такого рода служат чесальный рефлекс и рефлекс ходьбы. Когда обратная связь возможна и устойчива, то, как мы уже говорили, она даст ту выгоду, что делает поведение системы менее зависимым от нагрузки. Допустим, что нагрузка изменяет характеристику А на dА. Относительное изменение равно dA/A. Если оператор после обратной связи имеет вид то мы получим [с учетом 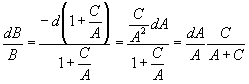 (4.52)
(4.52)
Таким образом, обратная связь позволяет уменьшить зависимость системы от характеристики двигателя и стабилизировать её для всех частот, для которых То есть вся граница между внутренними и внешними точками должна лежать внутри круга с радиусом С и центром в точке – С. Это не будет выполняться даже в первом из рассмотренных нами случаев. Эффект сильной отрицательной Обратной связи, если она устойчива, состоит в увеличении устойчивости системы при низких частотах, однако большей частью за счет её устойчивости при тех или иных высоких частотах. Тем не менее во многих случаях оказывается выгодной даже такая степень стабилизации. Рассмотрение колебаний, вызванных чрезмерной Обратной связью, поднимает весьма важный вопрос о частоте начинающегося колебания. Последняя определяется значением у в iy, соответствующим той точке границы между внутренней и внешней областями кривой (4.17), которая будет самой левой на отрицательной оси и. Величина у, очевидно, имеет размерность частоты. Мы пришли к концу нашего элементарного исследования линейных колебаний с точки зрения Обратной связи. Линейная колебательная система обладает весьма специальными свойствами, характеризующими её колебания. Одно из них заключается в том, что такая система всегда может и большей частью – при отсутствии независимых одновременных колебаний – будет совершать колебания вида Например, пусть Op[f(t)] – функция от f, полученная нелинейной операцией из f(t) и подвергаемая сдвигу. Тогда вариация δOp[f(t)] функции Op[f(t)], соответствующая вариационному изменению δf(t) функции f(t) и известному изменению динамики системы, является линейной, но неоднородной относительно δf(t), хотя она нелинейна относительно f(t). Если теперь мы знаем некоторое решение f(t) уравнения Op [f (t)] = 0 (4.55) и изменим динамику системы, то получим линейное неоднородное уравнение для δf(t). Если и сумма f(t)+δf(t) также периодическая, имея вид то Все коэффициенты в линейных уравнениях для δf(n) разлагаются в ряд по еiλnt, поскольку f(t) сама разложима в такой ряд. В результате получим бесконечную систему линейных неоднородных уравнений относительно δan+an, δλ и λ, и она может оказаться разрешимой методами Хилла. В этом случае можно, по крайней мере, представить, что, отправляясь от линейного (неоднородного) уравнения и понемногу снимая ограничения, мы можем прийти к решению весьма общей нелинейной задачи о релаксационных колебаниях. Однако это дело будущего. 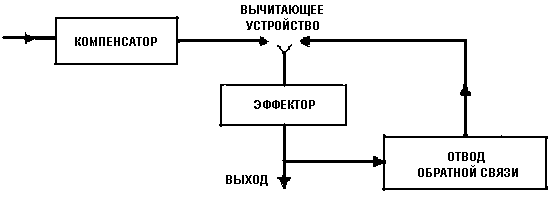 Системы
управления с Обратной связью, рассмотренные в этой главе, и
компенсационные системы, рассмотренные в предыдущей, до некоторой
степени конкурируют между собой. Те и другие служат для приведения
сложных отношений между входом и выходом эффектов к виду, близкому к
простой пропорциональности.
Как мы видели, система Обратной связи дает
большее: её поведение сравнительно независимо от характеристики
применяемого эффектора и изменений этой характеристики. Какой из двух
методов управления лучше, зависит, следовательно, от того, насколько
постоянна характеристика эффектора. Естественно предположить, что
могут быть случаи, когда выгодно сочетать оба метода. Для этого
существуют разные способы.
Один из
простейших показан на рис. 4. В этом случае всю систему Обратной связи
можно рассматривать как расширенный эффектор, и здесь не возникает
ничего нового, исключая то, что компенсатор должен компенсировать
величину, которая в некотором смысле является средней характеристикой
системы
обратной связи.
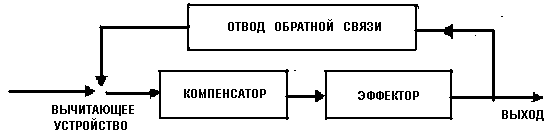
Другая
схема изображена на рис. 5. Здесь компенсатор и эффектор соединены в
один расширенный эффектор. Это, вообще
говоря, приводит к изменению максимально допустимой Обратной связи, и
нелегко сказать, насколько значительно можно повысить этот уровень таким
путем. С другой стороны, при том же уровне Обратной связи работа системы
совершенно явно улучшится. Если, например, эффектор имеет существенно
запаздывающую характеристику, то компенсатор должен быть упреждающим,
или предсказывающим, устройством, рассчитанным на статистический
ансамбль входного сигнала.
Обратная связь, которую можно назвать
упреждающей, будет стремиться ускорить действие эффектора. Системы
управления с Обратной связью, рассмотренные в этой главе, и
компенсационные системы, рассмотренные в предыдущей, до некоторой
степени конкурируют между собой. Те и другие служат для приведения
сложных отношений между входом и выходом эффектов к виду, близкому к
простой пропорциональности.
Как мы видели, система Обратной связи дает
большее: её поведение сравнительно независимо от характеристики
применяемого эффектора и изменений этой характеристики. Какой из двух
методов управления лучше, зависит, следовательно, от того, насколько
постоянна характеристика эффектора. Естественно предположить, что
могут быть случаи, когда выгодно сочетать оба метода. Для этого
существуют разные способы.
Один из
простейших показан на рис. 4. В этом случае всю систему Обратной связи
можно рассматривать как расширенный эффектор, и здесь не возникает
ничего нового, исключая то, что компенсатор должен компенсировать
величину, которая в некотором смысле является средней характеристикой
системы
обратной связи.
Другая
схема изображена на рис. 5. Здесь компенсатор и эффектор соединены в
один расширенный эффектор. Это, вообще
говоря, приводит к изменению максимально допустимой Обратной связи, и
нелегко сказать, насколько значительно можно повысить этот уровень таким
путем. С другой стороны, при том же уровне Обратной связи работа системы
совершенно явно улучшится. Если, например, эффектор имеет существенно
запаздывающую характеристику, то компенсатор должен быть упреждающим,
или предсказывающим, устройством, рассчитанным на статистический
ансамбль входного сигнала.
Обратная связь, которую можно назвать
упреждающей, будет стремиться ускорить действие эффектора.
 Обратные
связи подобного рода, несомненно, присутствуют в рефлексах человека и
животных. При охоте на уток мы стремимся свести к минимуму не ошибку
направления ствола относительно действительного положения цели, а
ошибку направления ствола относительно предугадываемого положения
цели. Всякая система управления зенитным огнем должна решать такую
же задачу. Условия устойчивости и эффективности упреждающих обратных
связей нуждаются в гораздо более тщательном исследовании, чем до сего
времени.
Другой
интересный вариант систем Обратной связи – управление автомобилем на
обледенелой дороге. Поведение водителя полностью определяется его
знанием, что дорога скользкая, т.е. знанием рабочих характеристик
системы автомобиль – дорога. Если он будет ждать, пока найдет эти
характеристики, ведя автомобиль обычным способом, то машину занесет,
прежде чем водитель опомнится. Поэтому он дает рулю последовательные
быстрые толчки – не такие сильные, чтобы вызвать большое скольжение, но
достаточные, чтобы его кинестетические ощущения дали ему знать, не
грозит ли автомобилю забрасывание, соответственно этому он и регулирует
свое вождение.
Этот метод
управления, который можно назвать управлением с помощью информирующей
обратной связи, нетрудно
воплотить в форму механизма, и он может оказаться полезным на практике.
Мы располагаем компенсатором для нашего эффектора, и этот компенсатор
имеет характеристику, которая изменима извне.
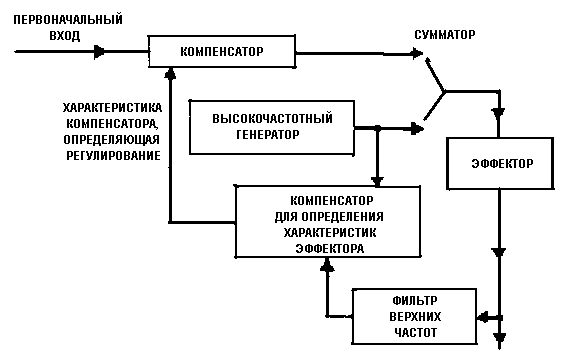
На приходящее сообщение
накладывается слабый высокочастотный сигнал, и от выходного сигнала
эффектора при помощи соответствующего фильтра отбирается некоторая часть
той же высокой частоты. Исследуется амплитудно-фазовая зависимость между
высокочастотным выходом и входом, чтобы найти рабочие характеристики
эффектора. На основании этого изменяют соответствующим образом
характеристики компенсатора.
Структурная схема системы будет выглядеть
примерно так, как на рис. 6. Обратные
связи подобного рода, несомненно, присутствуют в рефлексах человека и
животных. При охоте на уток мы стремимся свести к минимуму не ошибку
направления ствола относительно действительного положения цели, а
ошибку направления ствола относительно предугадываемого положения
цели. Всякая система управления зенитным огнем должна решать такую
же задачу. Условия устойчивости и эффективности упреждающих обратных
связей нуждаются в гораздо более тщательном исследовании, чем до сего
времени.
Другой
интересный вариант систем Обратной связи – управление автомобилем на
обледенелой дороге. Поведение водителя полностью определяется его
знанием, что дорога скользкая, т.е. знанием рабочих характеристик
системы автомобиль – дорога. Если он будет ждать, пока найдет эти
характеристики, ведя автомобиль обычным способом, то машину занесет,
прежде чем водитель опомнится. Поэтому он дает рулю последовательные
быстрые толчки – не такие сильные, чтобы вызвать большое скольжение, но
достаточные, чтобы его кинестетические ощущения дали ему знать, не
грозит ли автомобилю забрасывание, соответственно этому он и регулирует
свое вождение.
Этот метод
управления, который можно назвать управлением с помощью информирующей
обратной связи, нетрудно
воплотить в форму механизма, и он может оказаться полезным на практике.
Мы располагаем компенсатором для нашего эффектора, и этот компенсатор
имеет характеристику, которая изменима извне.
На приходящее сообщение
накладывается слабый высокочастотный сигнал, и от выходного сигнала
эффектора при помощи соответствующего фильтра отбирается некоторая часть
той же высокой частоты. Исследуется амплитудно-фазовая зависимость между
высокочастотным выходом и входом, чтобы найти рабочие характеристики
эффектора. На основании этого изменяют соответствующим образом
характеристики компенсатора.
Структурная схема системы будет выглядеть
примерно так, как на рис. 6.
 Этот вид
обратной связи выгоден тем, что компенсатор можно отрегулировать так,
чтобы обеспечить устойчивость при постоянной нагрузке любого рода, и
если характеристика нагрузки изменяется достаточно медленно, вековым,
как мы сказали, образом, по сравнению с изменениями первоначального
входного сигнала, а нагрузка замеряется точно, то система не будет
склонна к колебаниям.
Имеется много случаев, когда изменение нагрузки
является вековым в этом смысле. Например, трение орудийной башни зависит
от вязкости смазки, которая, в свою очередь, зависит от температуры, но
вязкость не изменится заметным образом в течение нескольких поворотов
башни.
Конечно,
связь будет работать хорошо только в том случае, когда характеристики
нагрузки на высоких частотах такие же, как на низких, или дают верное
отражение последних. Это часто имеет место, когда нагрузка, а значит, и
эффектор зависят от сравнительно небольшого числа переменных параметров.
Информирующая обратная связь и приведенные выше примеры
обратной связи с
компенсаторами представляют лишь частные случаи весьма сложной теории,
пока ещё недостаточно разработанной. Вся эта область развивается
чрезвычайно быстро и заслуживает того, чтобы в ближайшем будущем на неё
обратили гораздо больше внимания.
Прежде чем
закончить главу, мы должны напомнить другое очень важное физиологическое
применение принципа
обратной связи. В многочисленных примерах так
называемого гомеостаза мы встречаемся с тем фактом, что обратная
связь не только участвует в физиологических явлениях, но и оказывается
совершенно необходимой для продолжения жизни. Условия, при которых у
высших животных возможна жизнь, особенно нормальная жизнь, довольно
ограниченны. Изменение температуры тела на полградуса по Цельсию обычно
есть признак болезни, а при длительном изменении температуры на пять
градусов жизнь вряд ли возможна.
Осмотическое давление крови и
концентрация в ней водородных ионов должны поддерживаться в узких
границах. Отбросы организма должны извергаться, прежде чем они достигнут
токсической концентрации. Кроме того, у нас должно быть надлежащее
количество лейкоцитов и химических агентов защиты от инфекции; скорость
сердечных сокращений и кровяное давление должны быть не слишком высокими
и не слишком низкими; цикл половой деятельности должен соответствовать
потребностям воспроизведения рода; обмен кальция должен быть таким,
чтобы кости не размягчались и ткани не кальцинировались и т.д. Одним
словом, наше внутреннее хозяйство должно включать в себя целую батарею
термостатов, автоматических регуляторов давления и тому подобных
приборов – батарею, которой хватило бы на большой химический завод. Все
это вместе и составляет наш гомеостатический механизм.
Гомеостатические обратные связи имеют одно общее отличие от обратных
связей произвольных движений и обратных связей поз: они действуют
медленнее. Изменения физиологического гомеостаза, вызывающие
серьезное или постоянное нарушение в долю секунды, очень
немногочисленны, и даже анемия головного мозга действует не столь
стремительно. Поэтому нервные волокна предназначенные для
гомеостатических связей, т.е. волокна симпатической и
парасимпатической систем, часто лишены миэлиновой оболочки и, как
известно, имеют значительно меньшую скорость передачи, чем волокна с
миэлиновой оболочкой.
Типичные гомеостатические эффекторы – гладкие
мышцы и железы – также действуют медленно по сравнению с
поперечнополосатыми мышцами – типичными эффекторами произвольной
деятельности и деятельности, связанной с положением тела. Многие
сообщения гомеостатической системы передаются не по нервам, а по иным
каналам, таким, как непосредственный анастомоз мышечных волокон
сердца или химические вестники: гормоны, содержание углекислоты в крови
и т.д. За исключением сердечной мышцы, эти каналы передают сообщения
значительно медленнее, чем миэлинизированные нервные волокна.
Любой
полный курс кибернетики должен включать в себя тщательный и подробный
обзор гомеостатических процессов, которые во многих частных случаях
обсуждались в литературе довольно подробно.(2) Но данная книга
представляет собой более введение в предмет, нежели систематический
трактат; теория же гомеостатических процессов требует слишком детального
знакомства с общей физиологией, чтобы быть здесь к месту.
Примечания
1. Poincare H. Les Methodes Nouvelles de la Mecanique Celeste. – Paris:
Gauthier-Villars et fils., 1892–1899.
Этот вид
обратной связи выгоден тем, что компенсатор можно отрегулировать так,
чтобы обеспечить устойчивость при постоянной нагрузке любого рода, и
если характеристика нагрузки изменяется достаточно медленно, вековым,
как мы сказали, образом, по сравнению с изменениями первоначального
входного сигнала, а нагрузка замеряется точно, то система не будет
склонна к колебаниям.
Имеется много случаев, когда изменение нагрузки
является вековым в этом смысле. Например, трение орудийной башни зависит
от вязкости смазки, которая, в свою очередь, зависит от температуры, но
вязкость не изменится заметным образом в течение нескольких поворотов
башни.
Конечно,
связь будет работать хорошо только в том случае, когда характеристики
нагрузки на высоких частотах такие же, как на низких, или дают верное
отражение последних. Это часто имеет место, когда нагрузка, а значит, и
эффектор зависят от сравнительно небольшого числа переменных параметров.
Информирующая обратная связь и приведенные выше примеры
обратной связи с
компенсаторами представляют лишь частные случаи весьма сложной теории,
пока ещё недостаточно разработанной. Вся эта область развивается
чрезвычайно быстро и заслуживает того, чтобы в ближайшем будущем на неё
обратили гораздо больше внимания.
Прежде чем
закончить главу, мы должны напомнить другое очень важное физиологическое
применение принципа
обратной связи. В многочисленных примерах так
называемого гомеостаза мы встречаемся с тем фактом, что обратная
связь не только участвует в физиологических явлениях, но и оказывается
совершенно необходимой для продолжения жизни. Условия, при которых у
высших животных возможна жизнь, особенно нормальная жизнь, довольно
ограниченны. Изменение температуры тела на полградуса по Цельсию обычно
есть признак болезни, а при длительном изменении температуры на пять
градусов жизнь вряд ли возможна.
Осмотическое давление крови и
концентрация в ней водородных ионов должны поддерживаться в узких
границах. Отбросы организма должны извергаться, прежде чем они достигнут
токсической концентрации. Кроме того, у нас должно быть надлежащее
количество лейкоцитов и химических агентов защиты от инфекции; скорость
сердечных сокращений и кровяное давление должны быть не слишком высокими
и не слишком низкими; цикл половой деятельности должен соответствовать
потребностям воспроизведения рода; обмен кальция должен быть таким,
чтобы кости не размягчались и ткани не кальцинировались и т.д. Одним
словом, наше внутреннее хозяйство должно включать в себя целую батарею
термостатов, автоматических регуляторов давления и тому подобных
приборов – батарею, которой хватило бы на большой химический завод. Все
это вместе и составляет наш гомеостатический механизм.
Гомеостатические обратные связи имеют одно общее отличие от обратных
связей произвольных движений и обратных связей поз: они действуют
медленнее. Изменения физиологического гомеостаза, вызывающие
серьезное или постоянное нарушение в долю секунды, очень
немногочисленны, и даже анемия головного мозга действует не столь
стремительно. Поэтому нервные волокна предназначенные для
гомеостатических связей, т.е. волокна симпатической и
парасимпатической систем, часто лишены миэлиновой оболочки и, как
известно, имеют значительно меньшую скорость передачи, чем волокна с
миэлиновой оболочкой.
Типичные гомеостатические эффекторы – гладкие
мышцы и железы – также действуют медленно по сравнению с
поперечнополосатыми мышцами – типичными эффекторами произвольной
деятельности и деятельности, связанной с положением тела. Многие
сообщения гомеостатической системы передаются не по нервам, а по иным
каналам, таким, как непосредственный анастомоз мышечных волокон
сердца или химические вестники: гормоны, содержание углекислоты в крови
и т.д. За исключением сердечной мышцы, эти каналы передают сообщения
значительно медленнее, чем миэлинизированные нервные волокна.
Любой
полный курс кибернетики должен включать в себя тщательный и подробный
обзор гомеостатических процессов, которые во многих частных случаях
обсуждались в литературе довольно подробно.(2) Но данная книга
представляет собой более введение в предмет, нежели систематический
трактат; теория же гомеостатических процессов требует слишком детального
знакомства с общей физиологией, чтобы быть здесь к месту.
Примечания
1. Poincare H. Les Methodes Nouvelles de la Mecanique Celeste. – Paris:
Gauthier-Villars et fils., 1892–1899.2. Cannon W. The Wisdom of the Body. – New York: W.W. Norton & Company, Inc., 1932; 3. Henderson L.J. The Fitness of the Environment. – New York: The Macmillan Co., 1913. Оглавление www.pseudology.org |
|